David Andolfatto asks in a twitter exchange for evidence that deviations of GDP from trend are non-stationary. Here is the raw data. Figure 1 is the residual from a regression of the log of real GDP on a constant and a time trend for quarterly US data from 1955q1 through 2014q4. I will refer to this series as "X".
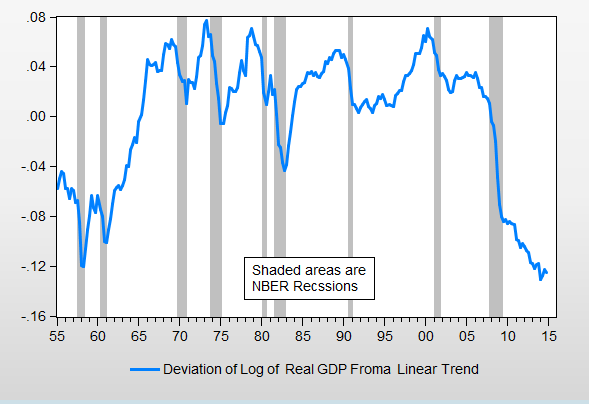
Figure 1: X = Log of Deviation of Real GDP from Trend
Table 1 reveals the regression of X on itself lagged and on a constant. Remember that these data describe deviations from trend so persistence reflects potentially permanent deviations from the trend growth path. Notice that the coefficient on lagged X is 0.996. That of course, does not establish that the data has a unit root.

Table 1: Regression Results
There are two approaches to testing formally for a unit root. For one group of tests, for example, the augmented Dickey Fuller test, the null hypothesis is that the series is non-stationary. For a second group, for example the KPSS test, the null hypothesis is that the series is stationary.
Table 2 presents the results of a Dickey Fuller test where the null hypothesis is that X has a unit root. Here we are looking for a test statistic that is small in absolute value if the series has a unit root, reflecting the fact that there is nothing pulling the series back towards trend.
The null hypothesis that X has a unit root cannot be rejected at the 1%, the 5% or the10% level.

Table 2: Augmented Dickey Fuller Test
The Dickey Fuller test is known to have very little power over the alternative of a root close to unity and sometimes it helps to look at additional evidence. Table 3 presents the KPSS test for which the null hypothesis is stationarity. Here we are looking for a large test statistic if the series has a unit root.
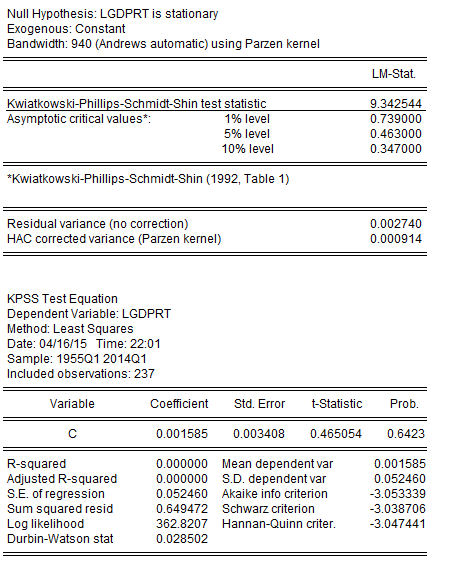
Table 3: KPSS Test
Notice that here, the null hypothesis of stationarity is overwhelmingly rejected.
What do we learn from this? Much the same as we learn from the fact that unemployment has a unit root. Just as unemployment can remain persistently high, so GDP can remain persistently below trend. There is no evidence that the economy is self-correcting.
